K Means
K-means clustering
TESTING BLOG Week 8 covers materials on unsupervised learning, which are learning algorithms that do not use class labels. It covers two topics: K-means clustering (an algorithm for detecting clusters in data) and principal component analysis (a dimension reduction algorithm).
Click here for the initial blog post on this series of lectures notes for the course
Click here for the initial blog post on this series of lectures notes for the course
K-means clustering is an algorithm for detecting clusters or groups in your data. The K refers to the pre-specified number of clusters that you want to detect in your data. It is an unsupervised learning algorithm because it doesn’t require your examples to have labels to detect the clusters. Some application of the K-means algorithm given in the course include market segmentation and social network analysis. Perhaps it can also be used to identify categories in your data in order to label them.
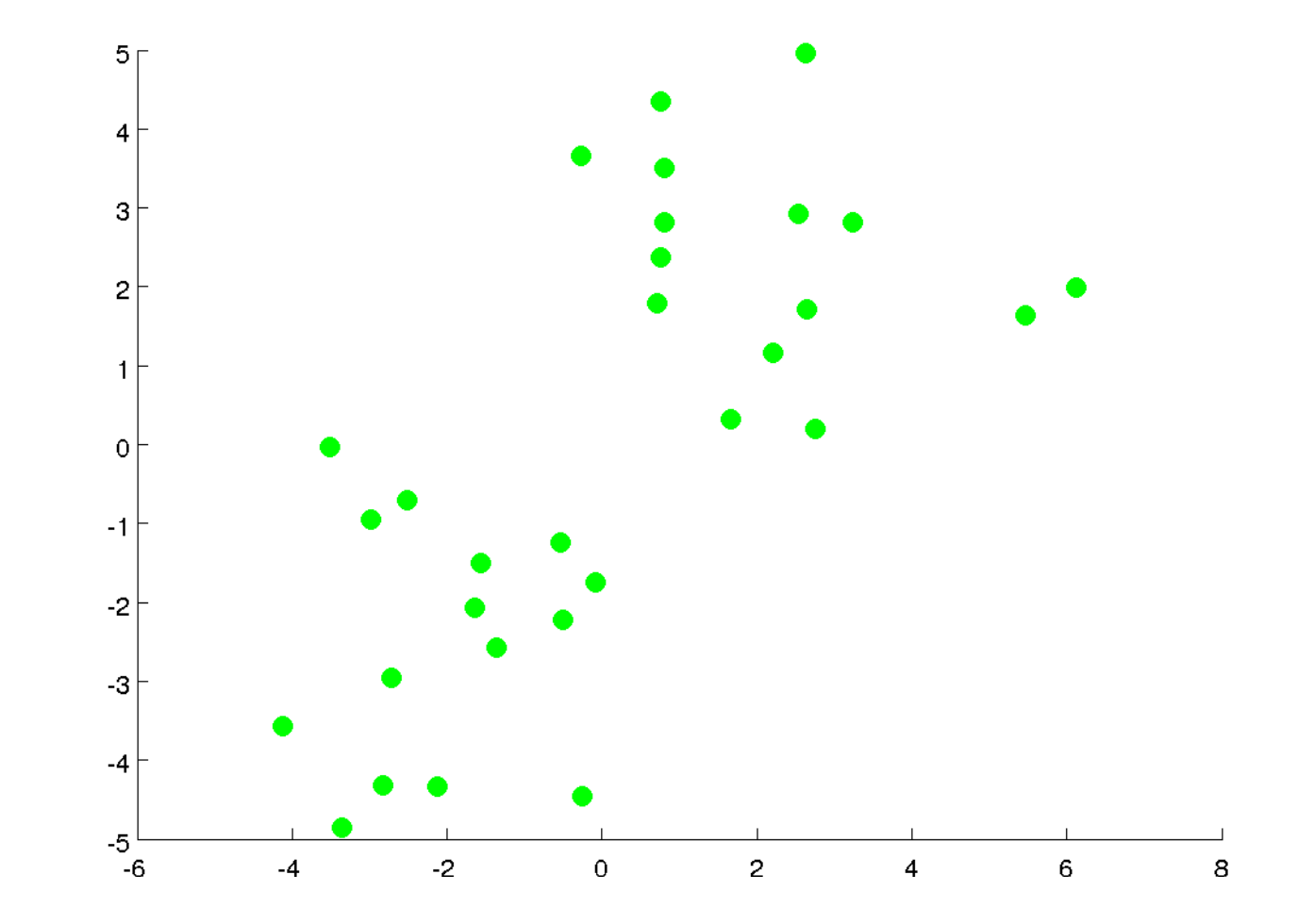
The goal is to get from data that look like this
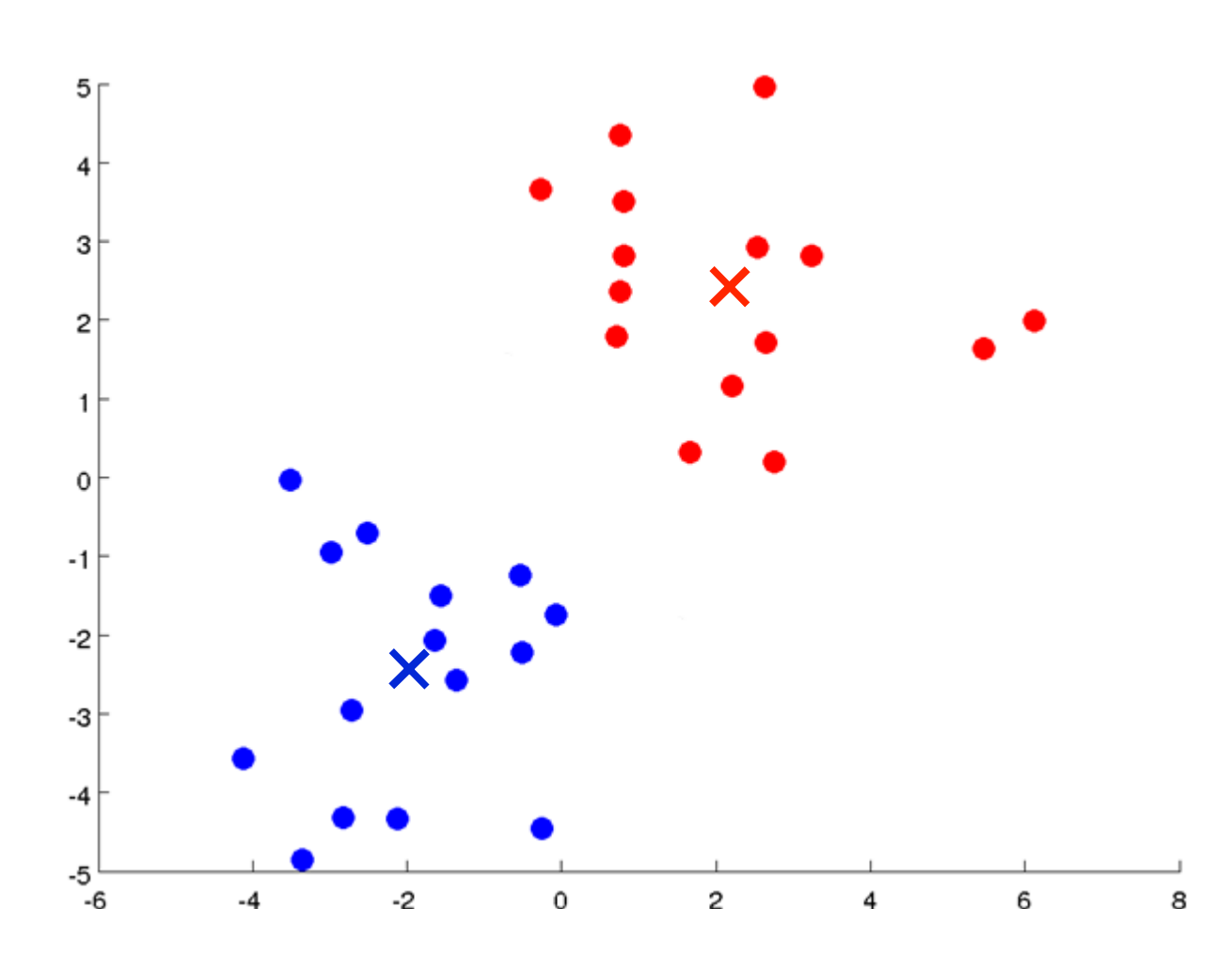
to data where groups are clearly identified
In the example above, it is easy enough to see that there are two clusters. But with data with a much larger set of features, it is harder to see. It is also not always the case that data organize themselves into obvious clusters
This is where a systematic approach for detecting clusters, which is what the K-means algorithm does, is useful.
The K-means clustering algorithm
Here is a description of the standard K-means algorithm described in the course:
- Choose the number of clusters K and randomly generate these K initial cluster centroid vectors.
-
For some prespecified number of iterations, do the following:
i. Assignment Step: assign each training example $x^{(i)}$ to one of the K-centroid it is closest to. Denote the optimal cluster centroid assigned to training example $i$ by $c^{(i)}$ . Formally, for each $x^{(i)}$, choose among the K vectors that minimizes the square of the norm of their difference: $min_{k} \lVert x^{(i)}-\mu_{k} \rVert^{2}$. ii. Update Step: Following i., each training example will be assigned to one of the K cluster centroid vectors. Calculate the K means of each of these group (e.g. if training examples 1, 5, 40, 53, and 106 are assigned to cluster centroid 2, then $\mu_{2} = (1 / 5) * (x^{(1)}+x^{(5)}+x^{(40)}+x^{(53)}+x^{(106)})$).
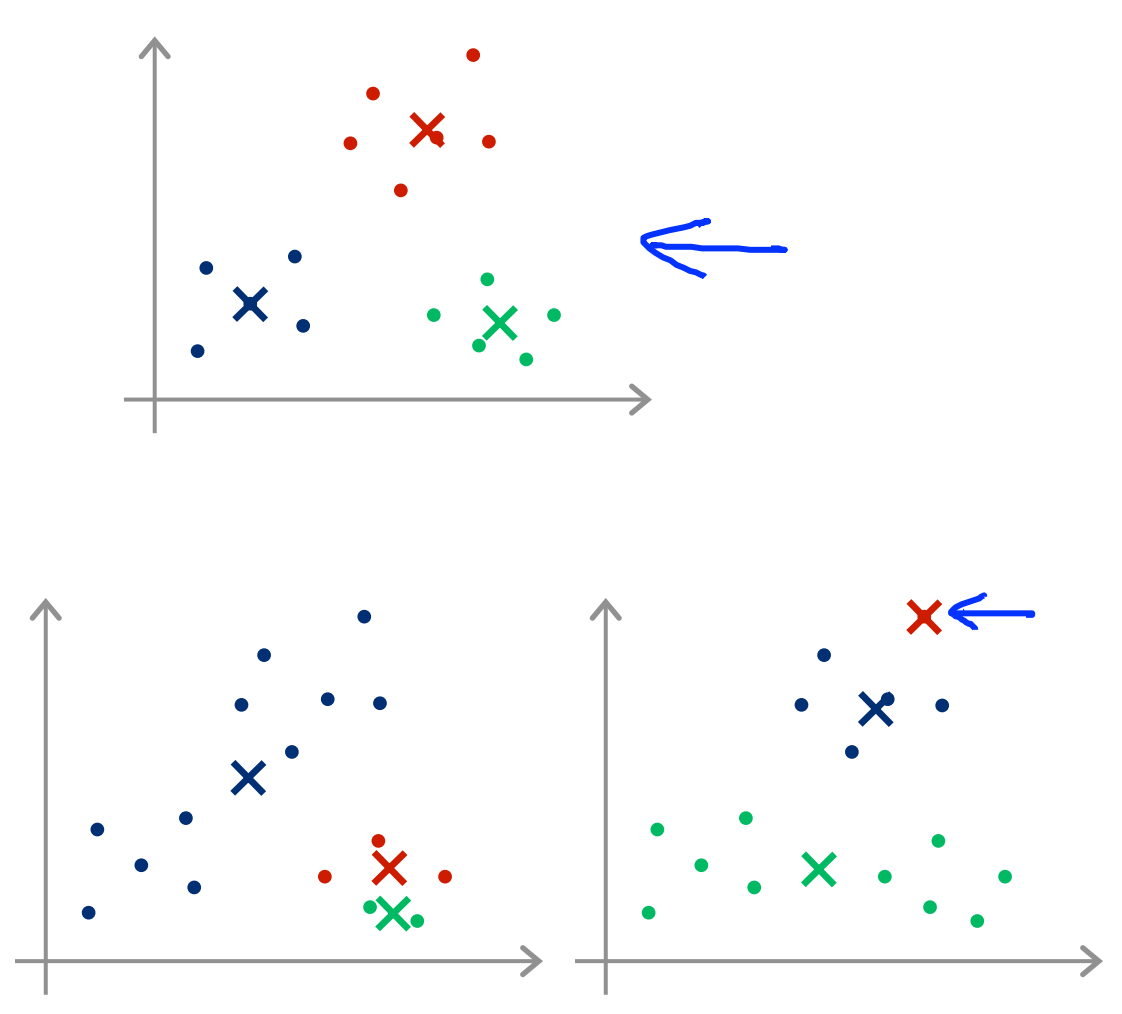
One issue that could arise with this algorithm is that it may converge to a local optima.
This happens if the initial K cluster centroids are poorly chosen. To fix this, use the following algorithm to run the K-means algorithm with different initializations of the K vectors:
- For some fixed number of iteration, Q:
- Randomly initialize the K vectors
- Run the standard algorithm described above and find the optimal assignments c^{(1)}, c^{(2)},…,c^{(m)} and K-means vectors $\mu_{1}, \mu_{2},…,\mu_{K}$ and the optimal assignments for each example
- Compute the cost function (distortion):
- $J(c^{(1)},…,c^{(m)}; \mu_{1},…,\mu_{K}) = (1/m) * \sum_{i=1}^{m} \lVert x^{(i)}-\mu_{c^{(i)}} \rVert^{2}$
- Among the Q costs calculated in 1., pick the assignments $c^{(1)}, c^{(2)},…,c^{(m)}$ and set of cluster centroids $\mu_{1}, \mu_{2},…,\mu_{K}$ that have the lowest cost.